Dưới đây là bài tập trắc nghiệm đồng biến nghịch biến của hàm số lớp 10 có đáp án và lời giải. Các bạn xem ở dưới.
Câu 1. Cho hàm số $f\left( x \right) = 4 – 3x$. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên $\left( { – \infty ;\frac{4}{3}} \right).$ B. Hàm số nghịch biến trên $\left( {\frac{4}{3}; + \infty } \right).$
C. Hàm số đồng biến trên $R.$ D. Hàm số đồng biến trên $\left( {\frac{3}{4}; + \infty } \right).$
Câu 2. Xét tính đồng biến, nghịch biến của hàm số $f\left( x \right) = {x^2} – 4x + 5$ trên khoảng $\left( { – \infty ;2} \right)$ và trên khoảng … Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên $\left( { – \infty ;2} \right)$, đồng biến trên $\left( {2; + \infty } \right)$.
B. Hàm số đồng biến trên $\left( { – \infty ;2} \right)$, nghịch biến trên $\left( {2; + \infty } \right)$.
C. Hàm số nghịch biến trên các khoảng $\left( { – \infty ;2} \right)$ và $\left( {2; + \infty } \right)$.
D. Hàm số đồng biến trên các khoảng $\left( { – \infty ;2} \right)$ và $\left( {2; + \infty } \right)$.
Câu 3. Xét sự biến thiên của hàm số $f\left( x \right) = \frac{3}{x}$ trên khoảng $\left( {0; + \infty } \right)$. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng $\left( {0; + \infty } \right).$
B. Hàm số nghịch biến trên khoảng $\left( {0; + \infty } \right).$
C. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng $\left( {0; + \infty } \right).$
D. Hàm số không đồng biến, cũng không nghịch biến trên khoảng $\left( {0; + \infty } \right).$
Câu 4. Xét sự biến thiên của hàm số $f\left( x \right) = x + \frac{1}{x}$ trên khoảng $\left( {1; + \infty } \right)$. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng $\left( {1; + \infty } \right).$
B. Hàm số nghịch biến trên khoảng $\left( {1; + \infty } \right).$
C. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng $\left( {1; + \infty } \right).$
D. Hàm số không đồng biến, cũng không nghịch biến trên khoảng $\left( {1; + \infty } \right).$
Câu 5. Xét tính đồng biến, nghịch biến của hàm số $f\left( x \right) = \frac{{x – 3}}{{x + 5}}$ trên khoảng $\left( { – \infty ; – 5} \right)$ và trên khoảng $\left( { – 5; + \infty } \right)$. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên $\left( { – \infty ; – 5} \right)$, đồng biến trên $\left( { – 5; + \infty } \right)$.
B. Hàm số đồng biến trên $\left( { – \infty ; – 5} \right)$, nghịch biến trên $\left( { – 5; + \infty } \right)$.
C. Hàm số nghịch biến trên các khoảng $\left( { – \infty ; – 5} \right)$ và $\left( { – 5; + \infty } \right)$.
D. Hàm số đồng biến trên các khoảng $\left( { – \infty ; – 5} \right)$ và $\left( { – 5; + \infty } \right)$.
Câu 6. Cho hàm số $f\left( x \right) = \sqrt {2x – 7} .$ Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên $\left( {\frac{7}{2}; + \infty } \right)$. B. Hàm số đồng biến trên $\left( {\frac{7}{2}; + \infty } \right).$
C. Hàm số đồng biến trên $R.$ D. Hàm số nghịch biến trên $R.$
Câu 7. Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $\left[ { – 3;3} \right]$ để hàm số $f\left( x \right) = \left( {m + 1} \right)x + m – 2$ đồng biến trên $R.$
A. $7.$ B. $5.$ C. $4.$ D. $3.$
Câu 43. Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = – {x^2} + \left( {m – 1} \right)x + 2$ nghịch biến trên khoảng $\left( {1;2} \right)$.
A. $m < 5.$ B. $m > 5.$ C. $m < 3.$ D. $m > 3.$
Câu 8. Cho hàm số $y = f\left( x \right)$ có tập xác định là $\left[ { – 3;3} \right]$ và đồ thị của nó được biểu diễn bởi hình bên.
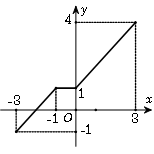
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng $\left( { – 3; – 1} \right)$ và $\left( {1;3} \right).$
B. Hàm số đồng biến trên khoảng $\left( { – 3; – 1} \right)$và $\left( {1;4} \right).$
C. Hàm số đồng biến trên khoảng $\left( { – 3;3} \right).$
D. Hàm số nghịch biến trên khoảng $\left( { – 1;0} \right).$
Câu 9. Cho đồ thị hàm số $y = {x^3}$ như hình bên.
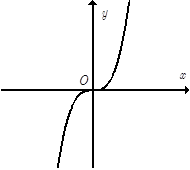
Khẳng định nào sau đây sai?
A. Hàm số đồng biến trên khoảng $\left( { – \infty ;0} \right).$
B. Hàm số đồng biến trên khoảng $\left( {0; + \infty } \right).$
C. Hàm số đồng biến trên khoảng $\left( { – \infty ; + \infty } \right).$
D. Hàm số đồng biến tại gốc tọa độ $O$.
LỜI GIẢI:
Câu 1. TXĐ:. D= R
Với mọi ${x_1},{x_2} \in R$ và ${x_1} < {x_2}$, ta có $ = – 3\left( {{x_1} – {x_2}} \right) > 0$
Suy ra $f\left( {{x_1}} \right) > f\left( {{x_2}} \right)$. Do đó, hàm số nghịch biến trên .
Mà $\left( {\frac{4}{3}; + \infty } \right) \subset R$ nên hàm số cũng nghịch biến trên $\left( {\frac{4}{3}; + \infty } \right)$. Chọn B.
Câu 2. Chọn A. Ta có $\left( {x_1^2 – 4{x_1} + 5} \right) – \left( {x_2^2 – 4{x_2} + 5} \right)$
$ = \left( {x_1^2 – x_2^2} \right) – 4\left( {{x_1} – {x_2}} \right) = \left( {{x_1} – {x_2}} \right)\left( {{x_1} + {x_2} – 4} \right)$.
● Với mọi và ${x_1} < {x_2}$. Ta có $\left\{ \begin{array}{l}
{x_1} < 2\\
{x_2} < 2
\end{array} \right. \Rightarrow {x_1} + {x_2} < 4$.
Suy ra $\frac{{f\left( {{x_1}} \right) – f\left( {{x_2}} \right)}}{{{x_1} – {x_2}}} = $$\frac{{\left( {{x_1} – {x_2}} \right)\left( {{x_1} + {x_2} – 4} \right)}}{{{x_1} – {x_2}}} = {x_1} + {x_2} – 4 < 0$ Vậy hàm số nghịch biến trên $\left( { – \infty ;2} \right)$. ● Với mọi ${x_1},{\rm{ }}{x_2} \in \left( {2; + \infty } \right)$ và . Ta có $\left\{ \begin{array}{l} {x_1} > 2\\
{x_2} > 2
\end{array} \right. \Rightarrow {x_1} + {x_2} > 4$.
Suy ra $\frac{{f\left( {{x_1}} \right) – f\left( {{x_2}} \right)}}{{{x_1} – {x_2}}} = $$\frac{{\left( {{x_1} – {x_2}} \right)\left( {{x_1} + {x_2} – 4} \right)}}{{{x_1} – {x_2}}} = {x_1} + {x_2} – 4 > 0$
Vậy hàm số đồng biến trên $\left( {2; + \infty } \right)$.
Câu 3. Ta có $f\left( {{x_1}} \right) – f\left( {{x_2}} \right) = \frac{3}{{{x_1}}} – \frac{3}{{{x_2}}}$$ = \frac{{3\left( {{x_2} – {x_1}} \right)}}{{{x_1}{x_2}}} = – \frac{{3\left( {{x_1} – {x_2}} \right)}}{{{x_1}{x_2}}}$
Với mọi ${x_1},{\rm{ }}{x_2} \in \left( {0; + \infty } \right)$ và ${x_1} < {x_2}$. Ta có $\left\{ \begin{array}{l} {x_1} > 0\\
{x_2} > 0
\end{array} \right. \Rightarrow {x_1}.x > 0$
Suy ra $\frac{{f\left( {{x_1}} \right) – f\left( {{x_2}} \right)}}{{{x_1} – {x_2}}} = – \frac{3}{{{x_1}{x_2}}} < 0 \Rightarrow f\left( x \right)$ nghịch biến trên $\left( {0; + \infty } \right)$. Chọn B.
Câu 4. Ta có
$f\left( {{x_1}} \right) – f\left( {{x_2}} \right) = \left( {{x_1} + \frac{1}{{{x_1}}}} \right) – \left( {{x_2} + \frac{1}{{{x_2}}}} \right)$$ = \left( {{x_1} – {x_2}} \right) + \left( {\frac{1}{{{x_1}}} – \frac{1}{{{x_2}}}} \right) = \left( {{x_1} – {x_2}} \right)\left( {1 – \frac{1}{{{x_1}{x_2}}}} \right)$
Với mọi ${x_1},{\rm{ }}{x_2} \in \left( {1; + \infty } \right)$ và ${x_1} < {x_2}$.
Ta có $\left\{ \begin{array}{l} {x_1} > 1\\
{x_2} > 1
\end{array} \right. \Rightarrow {x_1}.{x_1} > 1 \Rightarrow \frac{1}{{{x_1}.{x_1}}} < 1.$
Suy ra $\frac{{f\left( {{x_1}} \right) – f\left( {{x_2}} \right)}}{{{x_1} – {x_2}}} = 1 – \frac{1}{{{x_1}{x_2}}} > 0 \Rightarrow f\left( x \right)$ đồng biến trên $\left( {1; + \infty } \right)$. Chọn A.
Câu 5. Chọn D. Ta có $f\left( {{x_1}} \right) – f\left( {{x_2}} \right) = \left( {\frac{{{x_1} – 3}}{{{x_1} + 5}}} \right) – \left( {\frac{{{x_2} – 3}}{{{x_2} + 5}}} \right)$
$ = \frac{{\left( {{x_1} – 3} \right)\left( {{x_2} + 5} \right) – \left( {{x_2} – 3} \right)\left( {{x_1} + 5} \right)}}{{\left( {{x_1} + 5} \right)\left( {{x_2} + 5} \right)}}$ $ = \frac{{8\left( {{x_1} – {x_2}} \right)}}{{\left( {{x_1} + 5} \right)\left( {{x_2} + 5} \right)}}$
● Với mọi ${x_1},{\rm{ }}{x_2} \in \left( { – \infty ; – 5} \right)$ và ${x_1} < {x_2}$. Ta có$\left\{ \begin{array}{l}
{x_1} < – 5\\
{x_2} < – 5
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x_1} + 5 < 0\\
{x_2} + 5 < 0 \end{array} \right.$. Suy ra $\frac{{f\left( {{x_1}} \right) – f\left( {{x_2}} \right)}}{{{x_1} – {x_2}}} = \frac{8}{{\left( {{x_1} + 5} \right)\left( {{x_2} + 5} \right)}} > 0 \Rightarrow f\left( x \right)$ đồng biến trên $\left( { – \infty ; – 5} \right)$.
● Với mọi ${x_1},{\rm{ }}{x_2} \in \left( { – 5; + \infty } \right)$ và ${x_1} < {x_2}$. Ta có $\left\{ \begin{array}{l} {x_1} > – 5\\
{x_2} > – 5
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x_1} + 5 > 0\\
{x_2} + 5 > 0
\end{array} \right.$.
Suy ra $\frac{{f\left( {{x_1}} \right) – f\left( {{x_2}} \right)}}{{{x_1} – {x_2}}} = \frac{8}{{\left( {{x_1} + 5} \right)\left( {{x_2} + 5} \right)}} > 0$ $ \Rightarrow f\left( x \right)$đồng biến trên $\left( { – 5; + \infty } \right)$.
Câu 6. TXĐ: ${\rm{D}} = \left[ {\frac{7}{2}; + \infty } \right)$ nên ta loại đáp án C và D.
Xét $f\left( {{x_1}} \right) – f\left( {{x_2}} \right) = \sqrt {2{x_1} – 7} – \sqrt {2{x_2} – 7} $$ = \frac{{2\left( {{x_1} – {x_2}} \right)}}{{\sqrt {2{x_1} – 7} + \sqrt {2{x_2} – 7} }}$
Với mọi ${x_1},{\rm{ }}{x_2} \in \left( {\frac{7}{2}; + \infty } \right)$ và ${x_1} < {x_2}$, ta có $\frac{{f\left( {{x_1}} \right) – f\left( {{x_2}} \right)}}{{{x_1} – {x_2}}} = $$\frac{2}{{\sqrt {2{x_1} – 7} + \sqrt {2{x_2} – 7} }} > 0$
Vậy hàm số đồng biến trên $\left( {\frac{7}{2}; + \infty } \right)$. Chọn B.
Câu 7. Tập xác đinh ${\rm{D}} = R.$
Với mọi và ${x_1} < {x_2}$. Ta có $f\left( {{x_1}} \right) – f\left( {{x_2}} \right) = \left[ {\left( {m + 1} \right){x_1} + m – 2} \right]$$ – \left[ {\left( {m + 1} \right){x_2} + m – 2} \right] = \left( {m + 1} \right)\left( {{x_1} – {x_2}} \right)$ Suy ra $\frac{{f\left( {{x_1}} \right) – f\left( {{x_2}} \right)}}{{{x_1} – {x_2}}} = m + 1$. Để hàm số đồng biến trên R khi và chỉ khi $m + 1 > 0 \Leftrightarrow m > – 1$mà $m \in \left[ { – 3;3} \right],\,m \in Z$$ \Rightarrow m \in \left\{ {0;1;2;3} \right\}$
Vậy có 4 giá trị nguyên của $m$ thỏa mãn. Chọn C.
Câu 8. Với mọi , ta có
$\frac{{f\left( {{x_1}} \right) – f\left( {{x_2}} \right)}}{{{x_1} – {x_2}}} = $$\frac{{\left[ { – x_1^2 + \left( {m – 1} \right){x_1} + 2} \right] – \left[ { – x_2^2 + \left( {m – 1} \right){x_2} + 2} \right]}}{{{x_1} – {x_2}}}$$ = – \left( {{x_1} + {x_2}} \right) + m – 1$
Để hàm số nghịch biến trên $\left( {1;2} \right) \Leftrightarrow – \left( {{x_1} + {x_2}} \right) + m – 1 < 0$, với mọi ${x_1},{x_2} \in \left( {1;2} \right)$
$ \Leftrightarrow m < \left( {{x_1} + {x_2}} \right) + 1$, với mọi ${x_1},{x_2} \in \left( {1;2} \right)$
$ \Leftrightarrow m < \left( {1 + 1} \right) + 1 = 3$Chọn C.
Câu 9. Trên khoảng $\left( { – 3; – 1} \right)$ và $\left( {1;3} \right)$ đồ thị hàm số đi lên từ trái sang phải
Hàm số đồng biến trên khoảng $\left( { – 3; – 1} \right)$ và $\left( {1;3} \right).$ Chọn A.
Câu 10. Chọn D.




